Earl Zwicker Illinois Institute of Technology
Biological Chemical and Physical Sci Dept
IIT Center
Chicago IL 60616-3793
(312) 567-3384
Dedication: Thanks to Professor Harald Jensen (1898-1994), Physics
Department, Lake Forest College, who originally worked this idea with the
high school physics teachers at several summer institutes during the
1970s. This fine example of a phenomenological presentation would not
exist if it were not for him. Objectives:
For teachers (K - Phd): To model the phenomenological approach.
For students (grades 6 and above): To enable each student to prove the
Pythagorean Theorem on his own.
For students (grades K - 5): To enable students to identify, name and/or define
rectangle, square, triangle, and the concept of
area (a measure of the amount of surface).
Materials Needed:
Pieces for Pythagorean puzzle sawed from colored, transparent plastic
sheet (all the same thickness - about 1/8 inch - pieces of 4 different
colors). Optionally - several $100 Grand candy bars.
Sandwich bags, one for each person, each bag containing a set of the
puzzle pieces cut from brightly colored paper. (Use a machine to copy the
puzzle onto sheets of yellow paper and cut out.)
Performance assessment rubric.
Strategy:
For teachers: Ask: "Who has seen this before; anyone? Raise your hands."
If any hands are raised, then announce - "I need your help! If you have seen
or done this before, please do not give it away to those who have not. Please
don't spoil their fun."
Next, ask people to form pairs or partners by holding their hands up
together. Tell them to remember who their partner is.
1. Have the overhead projector prepared ahead of time by placing a blank
transparency centered on its projection area. Then begin by placing the
pieces of the puzzle on the overhead and viewing the image on a screen
so all can see and participate.
Challenge teachers to tell you how to assemble the pieces into a solid
rectangle using all the pieces - they must tell what to do; cannot show.
NOTE: Invariably, teachers - or almost anyone for that matter - will find it
difficult to tell you what to do. e.g. They might say, "Move the piece on top
next to the gray one." And you will move the piece, but not place them in
contact; or you will move the wrong piece, etc. You will not automatically do
what they want you to do, but rather only and literally what they
tell you to do. They will laugh to see how "stupid" you seem to be, but
they will see that you are doing only what they told you to do.
After 5 minutes or so, somebody might use the word "triangle" or "square"
or "rectangle" to describe the piece they wish you to move. As soon as one of
these words is used, repeat the word several times, (e.g. "triangle") and ask a
volunteer to define the word. Ask them to name the other pieces and get their
definition for each piece until everyone agrees and understands correctly the
names of the pieces. For triangles, make sure everyone agrees to the meanings
of "hypotenuse", "altitude", and "base".
This brings out the need for a common vocabulary, and the need to be able
to express one's thoughts with precision. If, then, someone asks you to move a
green triangle adjacent to the large, orange square, you will do so, but again,
the result is not what the person intended for you to do. You then might ask,
"Do you mean that you want me to move a green triangle so that its hypotenuse is
in continuous contact with an entire side of the large orange square?" If they
express agreement, then do it. Then see if others can express their thoughts
with precision by telling you what to do next. But once the point is made, do
not belabor it; go on to the next step.
2. Solve the puzzle.
See if they can direct you to the point where you have placed each of the
four identical triangles so that each has its hypotenuse congruent with one of
the four sides of the largest square, thus forming a single, solid
square. Once this is done, solving the puzzle will proceed rapidly. But
if more than 10 - 13 minutes have passed (aside from the digressions into the
need for vocabulary, etc.) and they still haven't solved the puzzle (which is
usually what happens), then pass out a sandwich bag of puzzle pieces to
each pair.
Then challenge each pair to complete the puzzle to form a solid rectangle
using their pieces. NOTE: If no pair succeeds within 5 minutes, then give a
hint: Using the pieces on the overhead, show them how to form the single, solid square mentioned in the previous paragraph. Then let them take it from
there with their paper puzzles. (See Sketch 1.)
The first pair to complete their puzzle should come up and show the rest
of us how, using the plastic pieces already on the overhead projector. (After
appropriate applause, etc. award them each a $100 Grand candy bar, which you
have kept out of sight.)
Then say: Thanks! Now all pairs complete your puzzles!
Everyone complete? OK!
Now let's see how good you really are.
3. Can you arrange your puzzle to form two squares of equal area, using all
the pieces? (There is an alternate solution to the first part where there
is an extra rectangle, in which case you omit the phrase 'using all of the
pieces' - but, until they ask, do not tell them that they do not need to use
one of the rectangles. See Sketch 2.)
Please do so now! (This will happen quickly for the pieces from sketch 1.)
Then - ask a pair to show their solution using the puzzle pieces already on
the overhead projector.
4. Say: You are now going to prove the Pythagorean theorem. Can anyone state
what it is?
After brief discussion, project a transparency of the Pythagorean
theorem in words:
For any right triangle, the square of the hypotenuse is equal to the
sum of the squares of the two sides. In other words:
If C is the length of the hypotenuse, and A is the length of its
altitude and B is the length of its base, then C2 = A2 + B2
5. The proof: With the two equal squares projected on the overhead for all to
see, show that they have equal areas by laying them on top of each
other. Make sure that the squares lie on the blank transparency.
Now place them along side each other, and using a felt marker pen,
draw an equal sign between them.
Next, remove two of the four triangles from one square, and one the
rectangles from the other. Show that the two triangles and the one
rectangle have equal areas (superposition is one easy way). Since we have
subtracted an equal amount of area from each of the originally equal
squares, the remaining areas must be equal on the left and right sides of
the equal sign.
Again, remove two more triangles from one side of the equal sign, and a
rectangle from the other side. Again, the remaining area on the left
side must equal the area remaining on the right side.
But on one side there will be a small square with the length of its side
equal to the base of a triangle, and a mid-size square with the length of
its side equal to the altitude of the same triangle. On the other side
will be a single largest square with the length of its side equal to the
hypotenuse of the same triangle. This is easily seen by placing the three
squares on the three appropriate sides of any one of the triangles.
Performance Assessment:
1. Hand out 2 blank pages and a copy of the rubric to each pair of teachers.
Say: I am going to ask each pair to use your puzzle to prove the Pythagorean
theorem. Do you want me to take a few minutes to review it? (They will
say yes.)
OK - there are four steps: 1. left square area = right square area
(Show them again.) 2. subtract equal areas from left and right
3. repeat
4. remainder areas are equal
2. Now - each pair write up the proof on your page. Use rough sketches to show
the four steps. You have about 7 minutes.
3. When finished, exchange your work with a neighboring pair and use the rubric
to score each others work.
References:
If the following graphic does not display or print, contact the author by
letter, telephone or email. NOTE: the puzzle should be scaled so that the
diagonal square is 3 inches on a side.
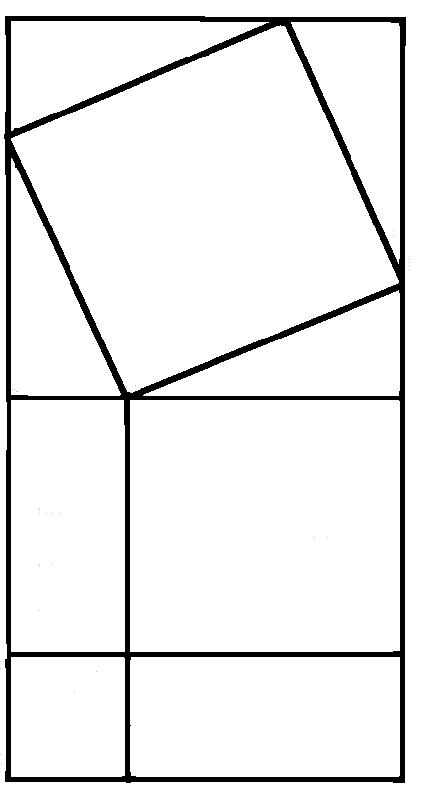
Sketch 1 In order to draw the puzzle on your own, use 2 sheets of 8.5 x 11 paper, a pencil, a ruler, a straight edge and a scissors. Draw a square three inches on a side. (This is easily done by starting at one corner of one of the papers and measuring 3 inches down each edge.) Cut out the square. Place the square so that its edges lie along the bottom right corner edges of the second sheet of paper. Now raise and tilt the square so that its right bottom corner has moved up the right edge of the page by about 1.5 inches; its left bottom corner should lie at the bottom edge of the page, about 2.5 inches from the right bottom corner of the page. The now tilted bottom of the square will be the hypotenuse of a right triangle, and the right bottom edges of the page will be the altitude and base of the triangle. Use some tape to hold the square in place on the sheet. Next, draw a horizontal line across the page so that it passes through the top-most corner of the tilted square. Then draw a vertical line so that it passes through the left-most corner of the tilted square. The square will now be circumscribed within a larger square formed by the horizontal and vertical lines drawn on the sheet. This also leaves the original tilted square surrounded by four identical triangles; the hypotenuses of the triangles are the four sides of the tilted square. For the upper-left triangle, draw a square using one of the triangles sides as one side of the square. Draw another square using the other side of the triangle. Now draw vertical lines through the vertical sides of the smallest square (on the left of the triangle). Then draw horizontal lines through the horizontal sides of the mid-size square (on the top of the triangle). You should now have formed three identical rectangles with long sides vertical (and equal in length to the altitude of the triangles), and short sides horizontal (and equal in length to the base of the triangles). Your puzzle is now complete. Cut it out and play with it. Enjoy!
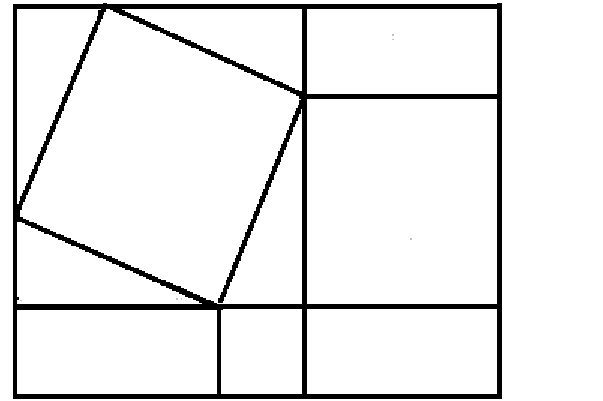
Sketch 2 (an 'extra' piece for the second part)